Unveiling The Geometry Of Vertical Angles: A Comprehensive Exploration

Unveiling the Geometry of Vertical Angles: A Comprehensive Exploration

Unveiling the Geometry of Vertical Angles: A Comprehensive Exploration

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Geometry of Vertical Angles: A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Geometry of Vertical Angles: A Comprehensive Exploration

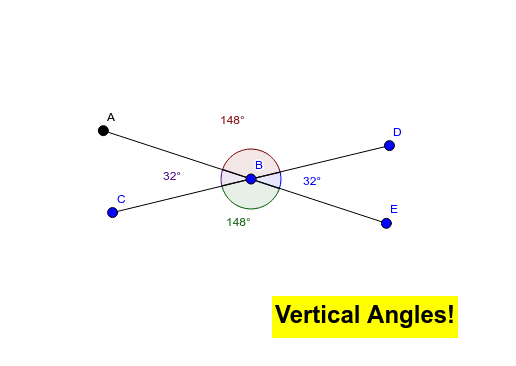
Vertical angles, a fundamental concept in geometry, play a crucial role in understanding the relationships between lines and angles. They are formed when two lines intersect, creating four distinct angles. This article delves into the properties of vertical angles, their significance in geometric proofs and problem-solving, and their practical applications in various fields.

Understanding the Concept of Vertical Angles

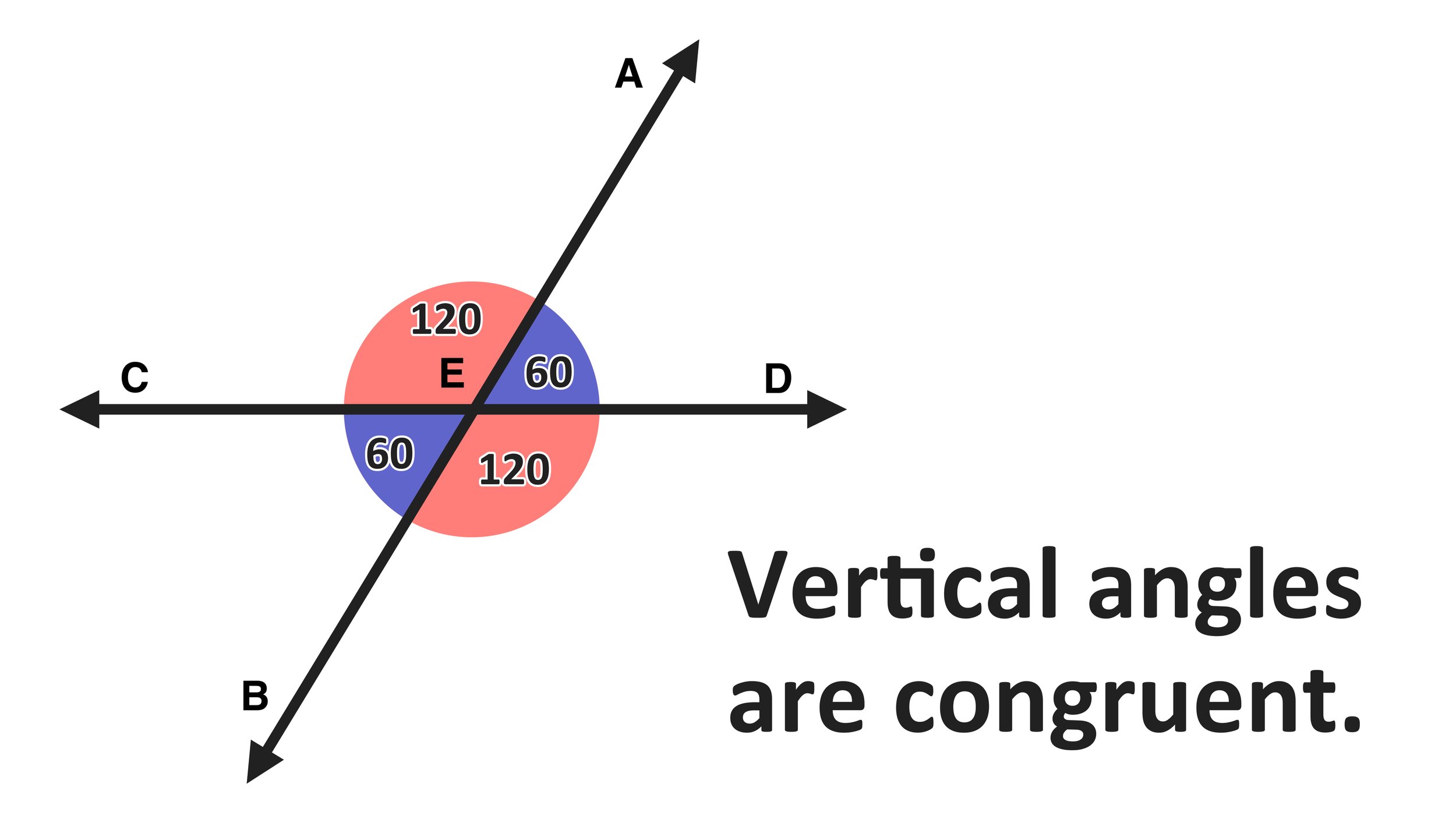
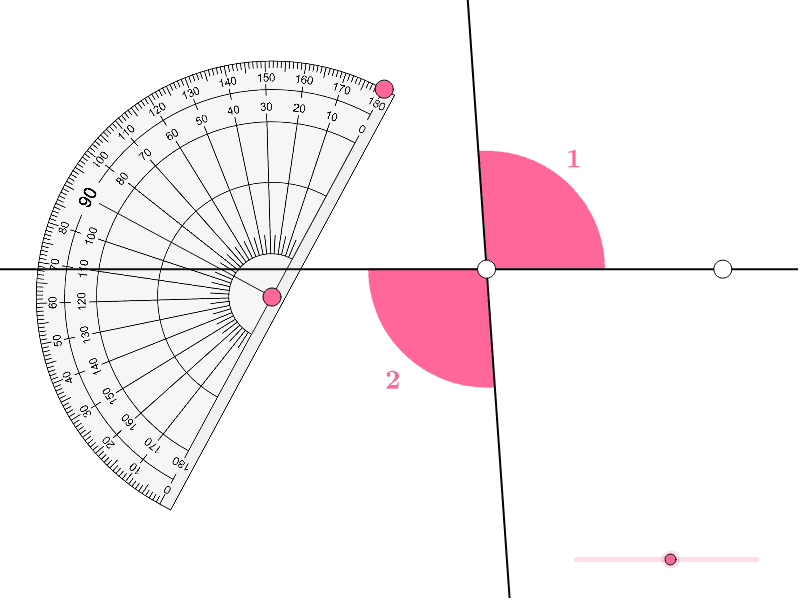
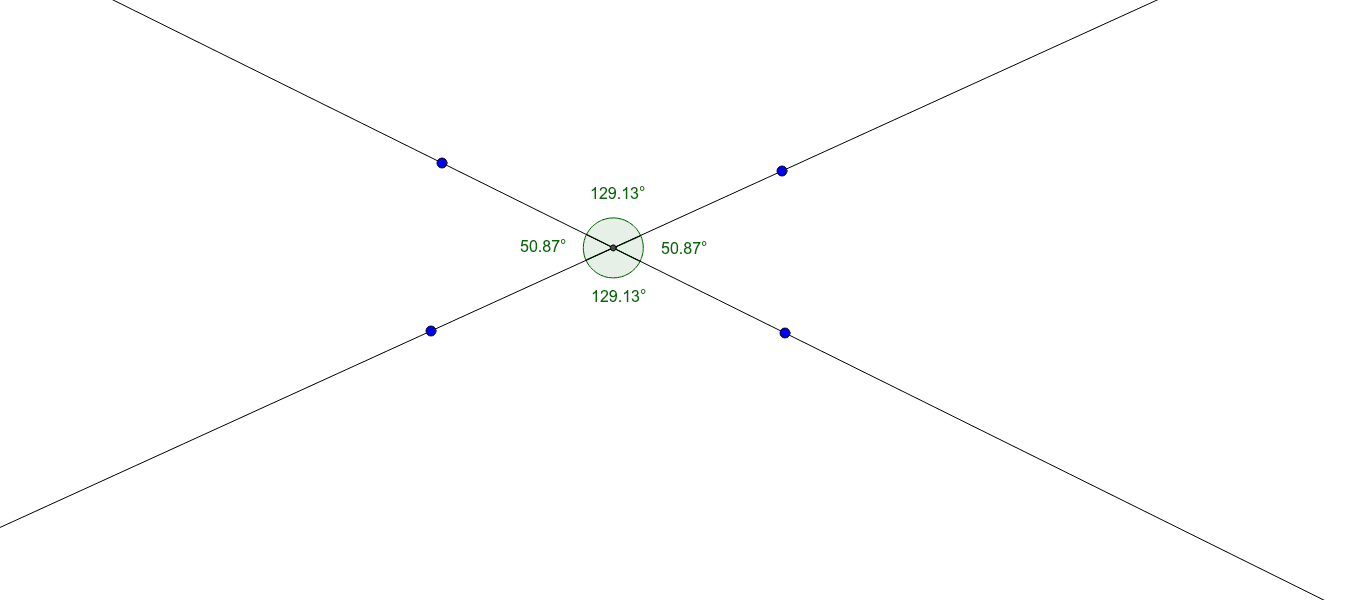
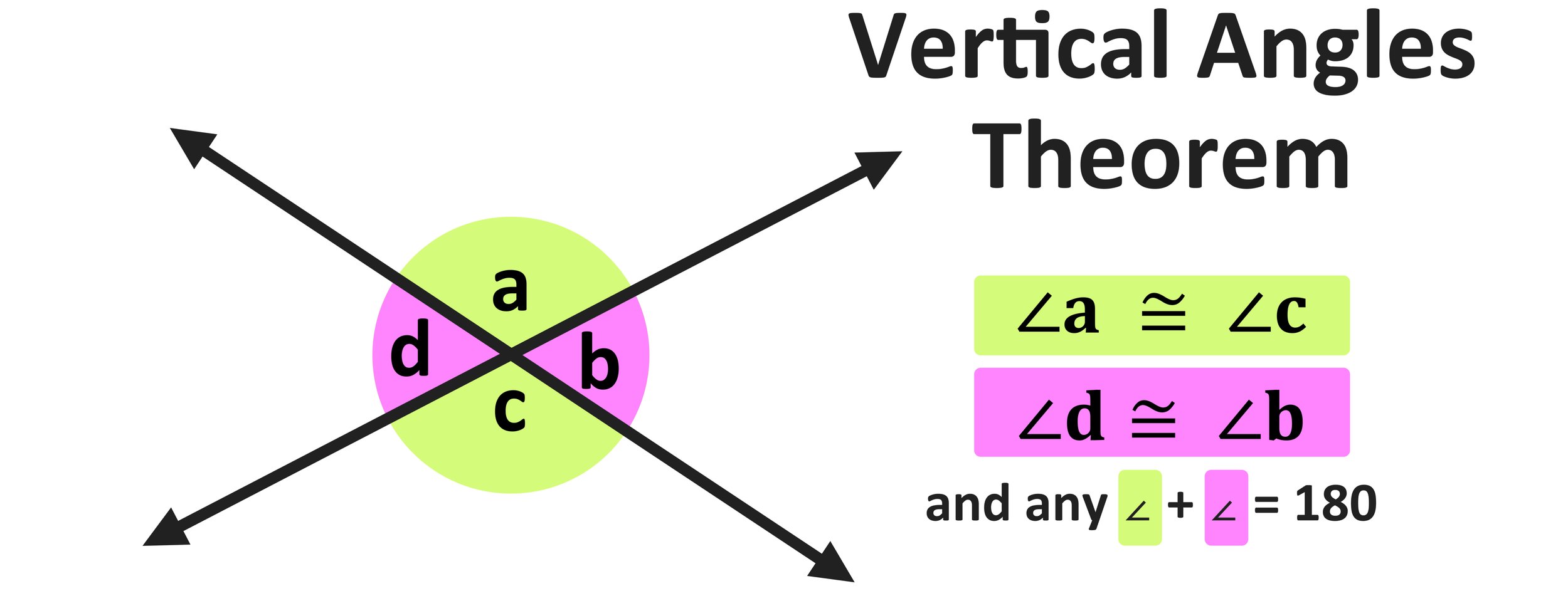
When two lines intersect, they create four distinct angles. Vertical angles are the pairs of opposite angles formed at the point of intersection. Imagine two straight lines crossing each other like an "X." The angles directly across from each other are vertical angles.

Key Properties of Vertical Angles

• Equal in Measure: The most important property of vertical angles is that they are always equal in measure. This means that if one vertical angle measures 60 degrees, the angle directly opposite it will also measure 60 degrees.
• Supplementary Angles: Vertical angles are not supplementary (meaning they do not add up to 180 degrees). However, each vertical angle forms a supplementary pair with its adjacent angle.

Illustrative Examples

Consider two intersecting lines, line AB and line CD, intersecting at point O. This creates four angles: ∠AOD, ∠BOD, ∠AOC, and ∠BOC.

• Vertical Angle Pairs: ∠AOD and ∠BOC are a pair of vertical angles, as are ∠BOD and ∠AOC.
• Supplementary Angle Pairs: ∠AOD and ∠BOD are supplementary, as are ∠AOD and ∠AOC, and so on.

The Importance of Vertical Angles in Geometry

Vertical angles play a vital role in various geometric proofs and problem-solving scenarios. Here are some key applications:

• Proving Congruence: Vertical angles are often used to prove that triangles are congruent. If two triangles share a vertical angle, and their corresponding sides are equal, then the triangles are congruent by the Angle-Side-Angle (ASA) congruence theorem.
• Solving for Unknown Angles: Knowing that vertical angles are equal allows us to solve for unknown angles in diagrams. If one vertical angle is given, we can immediately determine the measure of the other.
• Analyzing Geometric Shapes: Vertical angles are used to analyze the properties of various geometric shapes like parallelograms, quadrilaterals, and polygons. Understanding the relationship between vertical angles can help determine the angles within these shapes.

Beyond the Classroom: Practical Applications of Vertical Angles

Vertical angles are not merely a theoretical concept. They have practical applications in various fields, including:

• Construction: Architects and engineers use vertical angles to ensure that structures are built at the correct angles and that supports are properly aligned.
• Navigation: Navigators use vertical angles to determine the direction of travel and to calculate distances.
• Surveying: Surveyors use vertical angles to measure the elevation of land and to create maps.

Frequently Asked Questions

Q: Can vertical angles be supplementary?

A: No, vertical angles cannot be supplementary. While they share a common vertex, they are opposite angles and are therefore equal in measure.

Q: How are vertical angles related to adjacent angles?

A: Vertical angles are not directly related to adjacent angles. However, each vertical angle forms a supplementary pair with its adjacent angle.

Q: What are some real-world examples of vertical angles?

A: Examples of vertical angles abound in our daily lives. Think of the intersection of two roads, the crossing of two beams in a structure, or the hands of a clock when they form a right angle.

Tips for Understanding Vertical Angles

• Visualize: Draw diagrams to help you visualize the concept of vertical angles and their relationship with other angles.
• Practice: Solve problems involving vertical angles to reinforce your understanding and develop your problem-solving skills.
• Apply the Properties: Remember that vertical angles are equal in measure and use this property to solve problems.

Conclusion

Vertical angles are a fundamental concept in geometry that plays a crucial role in understanding the relationships between lines and angles. Their properties, applications, and importance in various fields highlight their significance in both theoretical and practical contexts. By understanding the concept of vertical angles, we gain valuable insights into the world of geometry and its applications in our daily lives.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Geometry of Vertical Angles: A Comprehensive Exploration. We thank you for taking the time to read this article. See you in our next article!